Loss & Cost Functions

-

Loss Functions

In neural networks, after a forward propagation, the loss function is calculated. The loss function is the result of the difference between actual output and the predicted output.

Different loss functions will return different values for the same prediction, and thus have a considerable effect on model performance.\

Regression Loss Functions
  • Mean Squared Error Loss
  • Mean Squared Logarithmic Error Loss
  • Mean Absolute Error Loss
Binary Classification Loss Functions
  • Binary Cross-Entropy
  • Hinge Loss
  • Squared Hinge Loss
Multi-Class Classification Loss Functions
  • Multi-Class Cross-Entropy Loss
  • Sparse Multiclass Cross-Entropy Loss
  • Kullback Leibler Divergence Loss

Cost Functions

Cost functions for Regression problems:
  • Mean Error (ME)
  • Mean Squared Error (MSE)
  • Mean Absolute Error (MAE)
  • Root Mean Squared Error (RMSE)
  • Categorical Cross Entropy Cost Function.
  • Binary Cross Entropy Cost Function.

Mean Absolute Error

This function returns the mean of absolute differences among predictions and actual values where all individual deviations have even importance.

Mean Square Error

This is the most commonly used loss function and also similar to MAE, this returns the square of the difference of actual and predicted values.

Root Mean Square Error

This is an extension of MSE, this returns as the average of the square root of the sum of squared differences between predictions and actual observations.

Binary cross-entropy

Binary cross entropy measures how far away from the true value (which is either 0 or 1) the prediction is for each of the classes and then averages these class-wise errors to obtain the final loss. We can see that p is compared to log-q(x) which will find the distance between the two.
Cross entropy will work best when the data is normalized (forced between 0 and 1) as this will represent it as a probability. This normalization property is common in most cost functions.

Categorical cross-entropy

This is a loss function that is used for single label categorization. This is when only one category is applicable to each data point. Use categorical cross-entropy in classification problems where only one result can be correct. Categorical cross-entropy will compare the distribution of the predictions (the activations in the output layer, one for each class) with the true distribution, where the probability of the true class is set to 1 and 0 for the other classes. To put it in a different way, the true class is represented as a one-hot encoded vector, and the closer the model’s outputs are to that vector, the lower the loss.


Hinge Loss

The function max(0,1-t) is called the hinge loss function. It is equal to 0 when t≥1. Its derivative is -1 if t<1 and 0 if t>1. It is not differentiable at t=1. but we can still use gradient descent using any subderivative at t=1. It is used in binary classification problems. It is used in the SVM problem. 
Hinge Loss not only penalizes the wrong predictions but also the right predictions that are not confident. Hinge loss output the value ranges from -inf to 1. Hinge loss is used for maximum-margin classification. Though hinge loss is not differentiable, it’s the convex function which makes it easy to work with usual convex optimizers used in the machine learning domain.

Multi-Class cross-entropy

Most time, Multi-class Cross-Entropy Loss is used as a loss function. The generalized form of cross-entropy loss is the multi-class cross-entropy loss.

where,
M - No of classes
y - binary indicator (0 or 1) if class label c is the correct classification for input o
p - predicted probability score of input o belonging to class c.

Kullback-Liebler Divergence LOSS (KL-Divergence)

  • KL Divergence is a measure of how a probability one distribution differs from another distribution.
  • Dkl(P||Q) is interpreted as the information gain when distribution Q is used instead of distribution P.
  • Dkl(Q||P) is interpreted as the information gain when distribution P is used instead of distribution Q.
  • Information gain (IG) measures how much “information” a feature gives us about the class.
  • KL Divergence is also known as “Relative entropy”. Dkl(P||Q) is read as Divergence from Q to P.
  • Dkl(P||Q) !=Dkl(Q||P). Divergence from Q to P is not symmetric to Divergence from P to Q.
  • Eg: Dkl(P||Q) =0.086 ;Dkl(Q||P)=0.096
  • It clear from the example that Dkl(P||Q) not symmetric to Dkl(Q||P).
  • 2. Dkl(P||P) =0 meaning both have identical distribution and not the information is gained from other distribution.
  • 3.The value of Dkl(P||Q) will be greater than or equal to zero.
  • So, the goal of the KL divergence loss is to approximate the true probability distribution P of our target variables with respect to the input features, given some approximate distribution Q. This Can be achieved by minimizing the Dkl(P||Q) then it is called forward KL. If we are minimizing Dkl(Q||P) then it is called backward KL.
  • Forward KL → applied in Supervised Learning
  • Backward KL → applied in Reinforcement learning



Notes

Q.Why KL divergence is not considered as a distance metric?
A. Reason is simple KL divergence is not symmetric.KL- Divergence is functionally similar to multi-class Cross entropy.

Q.What is the difference between an RMSE and RMSLE (logarithmic error), and does a high RMSE imply low RMSLE?
A. Root Mean Squared Error (RMSE) and Root Mean Squared Logarithmic Error (RMSLE) both are the techniques to find out the difference between the values predicted by your machine learning model and the actual values.
  1. If both predicted and actual values are small: RMSE and RMSLE is same.
  2. If either predicted or the actual value is big: RMSE > RMSLE
  3. If both predicted and actual values are big: RMSE > RMSLE (RMSLE becomes almost negligible)

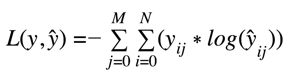
Comments

Post a Comment

Popular posts from this blog

Deep Learning

-
Image
Deep Learning What is Deep Learning? Deep learning is a subset of machine learning in artificial intelligence (AI) that has networks based learning from data that is unstructured or unlabeled. Also known as deep neural learning or deep neural network. This is also similar to the Human Brain. Do you know the First Neuron created? Yes, Perceptron is the first neural network unit, that does some computations to detect features and business intelligence in input data. This was introduced by  Frank Rosenblatt in 1957. Types of Deep Learning? Artificial Neural Network Deep Brief Net Convolutional Neural Network Recurrent Neural Network Neural Network The first layer is the Input Layer, next is the Hidden layer and the final one is the Output layer. there can be any number of hidden layers in the network. How Neural Network works? Neural Network we create works similar to the human brain, we give features th
Read more

Recurrent Neural Network & LSTM

-
Image
Recurrent Neural Network RNN is a neural network, where the output of the previous step is fed as input to the current step . The reason why the previous output is required in cases likes to predict the next word in the sentence, hence remembrance of previous words. Hence RNN has loops in them, allowing information (words) to persist. Here, A is a network, A gets an input X  and leaves an output value h.  A loop allows information to be passed from one step of the network to the next. RNN is multiple copies of the same network, each passing the same information to the successor. Applications of RNN Chat Bots NLP Translator Sentence completer Stock price Predictor, etc The problem in  Simple RNN The problem is Long-term Dependencies . For example, consider a language model trying to predict the next word based on the previous word. If we are trying to predict the last word in "The clouds are in the sky," we don’t need any further context – it’s pretty obvious the next word i
Read more